设函数
(1)求 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(3)画出函数 在区间
在区间 上的图像(完成列表并作图)。
上的图像(完成列表并作图)。
(1)列表
| x |
0 |
|
 |
|
 |
 |
| y |
|
-1 |
|
1 |
|
|
(2)描点,连线
选修4-4:坐标系与参数方程 在直角坐标系
在直角坐标系 中, 过点
中, 过点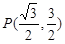 作倾斜角为
作倾斜角为 的直线
的直线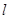 与曲线
与曲线 相交于不同的两点
相交于不同的两点 .
.
(Ⅰ) 写出直线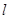 的参数方程; (Ⅱ) 求
的参数方程; (Ⅱ) 求 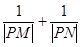 的取值范围.
的取值范围.
如图,  内接于⊙
内接于⊙ ,
,  是⊙
是⊙ 的直径,
的直径, 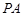 是过点
是过点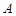 的直线, 且
的直线, 且 .
.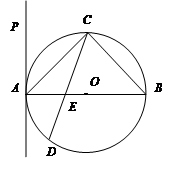
(Ⅰ) 求证: 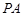 是⊙
是⊙ 的切线;
的切线;
(Ⅱ)如果弦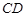 交
交 于点
于点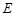 ,
, 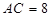 ,
,  ,
,  , 求
, 求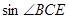 .
.
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,釆用分层抽样抽取了 105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校.
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
2 |
3 |
10 |
15 |
15 |
X |
3 |
1 |
乙校:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110] |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
1 |
2 |
9 |
8 |
10 |
10 |
y |
3 |
(1)计算x, y的值;
(2)由以上统计数据填写下面2X2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
附:
| P(k2>k0) |
0. 10 |
0. 025 |
0. 010 |
| K |
2. 706 |
5. 024 |
6. 635 |
已知函数f(x)= x
x -ax+(a-1)
-ax+(a-1) ,
, 。
。
(1)讨论函数 的单调性;
的单调性;
(2)证明:若 ,则对任意x
,则对任意x ,x
,x

 ,x
,x
 x
x ,有
,有 。
。
在一个盒子里放有6张卡片,上面标有数字1,2,3,4,5,6,现在从盒子里每次任意取出一张卡片,取两片.
(I)若每次取出后不再放回,求取到的两张卡片上数字之积大于12的概率;
(II)在每次取出后再放回和每次取出后不再放回这两种取法中,得到的两张卡片上的最大数字的期望值是否相等?请说明理由.