已知圆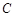 过点
过点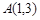 ,
,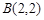 ,并且直线
,并且直线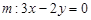 平分圆的面积.
平分圆的面积.
(1)求圆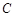 的方程;
的方程;
(2)若过点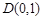 ,且斜率为
,且斜率为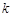 的直线
的直线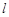 与圆
与圆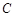 有两个不同的公共点
有两个不同的公共点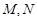 .
.
①求实数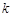 的取值范围; ②若
的取值范围; ②若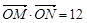 ,求
,求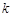 的值.
的值.
已知数列 满足
满足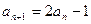 且
且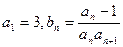 ,数列
,数列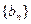 的前n项和为
的前n项和为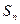 ,
,
(1)求证:数列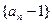 是等比数列;
是等比数列;
(2)求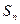 ;
;
(3)设 ,求证:
,求证: 。
。
设函数 ,
,
(1)令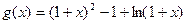 ,判断并证明
,判断并证明 在
在 上的单调性,并求
上的单调性,并求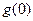 ;
;
(2)求函数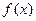 的最小值;
的最小值;
(3)是否存在实数m,n,满足-1<m<n,使得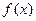 在区间[m,n]上的值域也为[m,n]。
在区间[m,n]上的值域也为[m,n]。
在平面内有两个向量 ,今有动点P从
,今有动点P从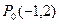 开始沿着与向量
开始沿着与向量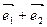 相同方向做匀速直线运动,速度为︱
相同方向做匀速直线运动,速度为︱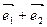 ︱;另一动点Q从点
︱;另一动点Q从点 (-2,-
(-2,- 1)出发,沿着与向量
1)出发,沿着与向量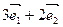 相同的方向做匀速直线运动,速度为︱
相同的方向做匀速直线运动,速度为︱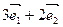 ︱,设点P、Q在时刻t=0秒时分别在
︱,设点P、Q在时刻t=0秒时分别在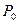 、
、 处,求PQ⊥
处,求PQ⊥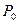
 时,用了多长时间
时,用了多长时间
已知向量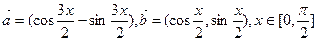 ,函数
,函数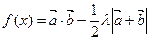

(1)若 ,求方程
,求方程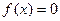 的根;
的根;
(2)若函数 的最小值为
的最小值为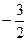 ,求实数
,求实数 的值。
的值。
已知锐角△ABC中,角 A.B.C所对边分别是a.b.c,
A.B.C所对边分别是a.b.c,
 ,且
,且 ∥
∥
(2)求角B的大小;
(3)如果b=1,求△ABC面积的最大值。