某高校共有学生15 000人，其中男生10 500人，女生4 500人，为调查该校学生每周平均体育运动的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为：[0,2],(2,4], (4,6], (6,8], (8,10], (10,12],估计该校学生每周平均体育运动时间超过4小时的概率；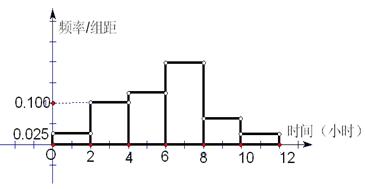
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
附：
| P(K2≥k0) |
0.10 |
0.05 |
0.010 |
0.005 |
| k0 |
2.706 |
3.841 |
6.635 |
7.879 |
已知圆C：x2＋y2＋x－6y＋m＝0与直线l：x＋2y－3＝0.
(1)若直线l与圆C没有公共点，求m的取值范围；
(2)若直线l与圆C相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值．
如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE＝3AF，BE与平面ABCD所成的角为60°. 
(1)求证：AC⊥平面BDE；
(2)求二面角F-BE-D的余弦值；
(3)设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．
如图所示的长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，O为AC与BD的交点，BB1＝
，M是线段B1D1的中点．
(1)求证：BM∥平面D1AC；
(2)求证：D1O⊥平面AB1C；
(3)求二面角B-AB1-C的大小．
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA1＝2，E，E1，F分别是棱AD，AA1，AB的中点．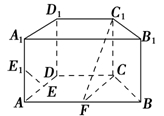
(1)证明：直线EE1∥平面FCC1；
(2)求二面角B-FC1-C的余弦值．
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.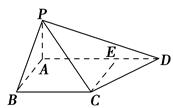 
(1)求证：CE⊥平面PAD；
(2)若PA＝AB＝1，AD＝3，CD＝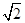
，∠CDA＝45°，求四棱锥P-ABCD的体积．