如图，矩形
的顶点
为原点，
边所在直线的方程为
，顶点
的纵坐标为
．
（1）求
边所在直线的方程；
（2）求矩形的面积．
(1)在(1＋x)n的展开式中，若第3项与第6项系数相等，则n等于多少？
(2)
的展开式奇数项的二项式系数之和为128，求展开式中二项式系数最大项．
用二次项定理证明32n＋2－8n－9能被64整除(n∈N)．
已知(2－
x)50＝a0＋a1x＋a2x2＋…＋a50x50，其中a0，a1，a2…，a50是常数，计算(a0＋a2＋a4＋…＋a50)2－(a1＋a3＋a5＋…＋a49)2.
已知
n展开式中的二项式系数的和比(3a＋2b)7展开式的二项式系数的和大128，求n展开式中的系数最大的项和系数最小的项．
已知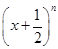
的展开式中前三项的系数成等差数列．设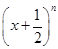＝a0＋a1x＋a2x2＋…＋anxn.求：
(1)a5的值；
(2)a0－a1＋a2－a3＋…＋(－1)nan的值；
(3)ai(i＝0，1，2，…，n)的最大值．