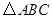 中,
中,  ,
, .
.
(1)若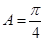 ,求
,求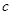 ;(2)若
;(2)若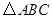 的面积S=
的面积S= ,求
,求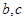 。
。
解下列不等式:
(1)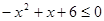
(2)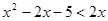
已知数列 的前n项和为
的前n项和为 ,
, ,且
,且 是
是 与1的等差中项.
与1的等差中项.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若数列 的前n项和为
的前n项和为 ,且对任意
,且对任意 ,
, 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
在平行四边形ABCD中, ,边AB、AD的长分别为2、1. 若M、N分别是边BC、CD上的点,且满足
,边AB、AD的长分别为2、1. 若M、N分别是边BC、CD上的点,且满足 ,求
,求 的取值范围.
的取值范围.
某赛事组委会要为获奖者定做某工艺品作为奖品,其中一等奖奖品3件,二等奖奖品6件.制作一等奖和二等奖奖品所用原料完全相同,但工艺不同,故价格有所差异.现有甲、乙两家工厂可以制作奖品(一等奖、二等奖奖品均符合要求),甲厂收费便宜,但原料有限,最多只能制作4件奖品,乙厂原料充足,但收费交贵,其具体收费情况如下表:
求组委会定做该工艺品至少需要花费多少元钱.