已知函数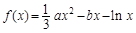 ,其中a,b∈R
,其中a,b∈R
(1)当a=3,b=-1时,求函数f(x)的最小值;
(2)若曲线y=f(x)在点(e,f(e))处的切线方程为2x-3y-e=0(e=2.71828 为自然对数的底数),求a,b的值;
(3)当a>0,且a为常数时,若函数h(x)=x[f(x)+lnx]对任意的x1>x2≥4,总有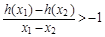 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围.
命题甲:  R, 关于x的方程
R, 关于x的方程 有两个非零实数解;
有两个非零实数解;
命题乙:  R, 关于x的不等式
R, 关于x的不等式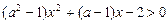 的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
集合A是由具备下列性质的函数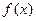 组成的:
组成的:
(1) 函数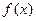 的定义域是
的定义域是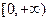 ;
;
(2) 函数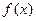 的值域是
的值域是 ;
;
(3) 函数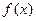 在
在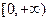 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(Ⅰ)判断函数 ,及
,及 是否属于集合A?并简要说明理由.
是否属于集合A?并简要说明理由.
(Ⅱ)对于(I)中你认为属于集合A的函数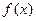 ,不等式
,不等式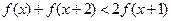 ,是否对于任意的
,是否对于任意的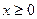 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.
解关于 的不等式
的不等式 ,其中
,其中 .
.
已知函数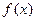 是定义在
是定义在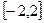 上的奇函数,当
上的奇函数,当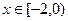 时,
时, (
( 为常数)。
为常数)。
(1)求函数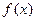 的解析式;
的解析式;
(2)当 时,求
时,求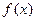 在
在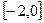 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的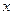 ,并猜想
,并猜想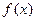 在
在 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当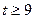 时,证明:函数
时,证明:函数 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线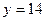 上。
上。
设函数f(x)的定义域D关于原点对称,0∈D,且存在常数a>0,使f(a)=1,又 ,
,
(1)写出f(x)的一个函数解析式,并说明其符合题设条件;
(2)判断并证明函数f(x)的奇偶性;
(3)若存在正常数T,使得等式f(x)=f(x+T)或者f(x)=f(x-T)对于x∈D都成立,则都称f(x)是周期函数,T为周期;试问f(x)是不是周期函数?若是,则求出它的一个周期T;若不是,则说明理由。