某工厂某种产品的年产量为1000x件,其中x∈[20,100],需要投入的成本为C(x),当x∈[20,80]时,C(x)=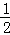 x2﹣30x+500(万元);当x∈(80,100]时,C(x)=
x2﹣30x+500(万元);当x∈(80,100]时,C(x)=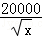 (万元).若每一件商品售价为
(万元).若每一件商品售价为 (万元),通过市场分析,该厂生产的商品能全部售完.
(万元),通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于x的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
已知
(1)讨论 的单调性;
的单调性;
(2)当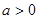 时,若对于任意
时,若对于任意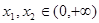 ,都有
,都有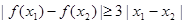 ,求
,求 的取值范围.
的取值范围.
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽查了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.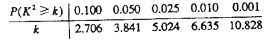
| 月收入(单位百元) |
[15,25 |
[25,35 |
[35,45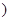 |
[45,55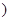 |
[55,65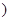 |
[65,75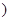 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
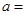 |
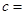 |
|
| 不赞成 |
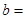 |
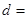 |
|
| 合计 |
(2)若对月收入在[15,25) ,[25,35)的被调查人中各随机选取1人进行追踪调查,求选中的2人中不赞成“楼市限购令”人数至多1人的概率。
参考数据: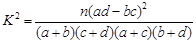
已知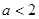 ,函数
,函数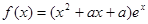
(1)当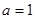 时,求
时,求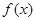 的单调递增区间;
的单调递增区间;
(2)若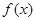 的极大值是
的极大值是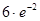 ,求
,求 的值.
的值.
已知函数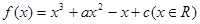 ,下列结论错误的是()
,下列结论错误的是()
A.函数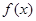 一定存在极大值和极小值 一定存在极大值和极小值 |
B.若函数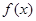 在 在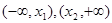 上是增函数,则 上是增函数,则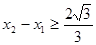 |
C.函数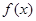 的图像是中心对称图形 的图像是中心对称图形 |
D.函数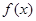 一定存在三个零点 一定存在三个零点 |
已知函数f(x)=-x3+ax2+1(a∈R).
(1)若函数y=f(x)在区间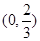 上递增,在区间
上递增,在区间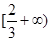 上递减,求a的值;
上递减,求a的值;
(2)当x∈[0,1]时,设函数y=f(x)图象上任意一点处的切线的倾斜角为θ,若给定常数a∈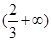 ,求
,求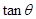 的取值范围;
的取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数g(x)=x4-5x3+(2-m)x2+1(m∈R)的图象与函数y=f(x)的图象恰有三个交点.若存在,求实数m的取值范围;若不存在,试说明理由.