小锦和小丽购买了价格分别相同的中性笔和笔芯,小锦买了20支笔和2和盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元。求每支中性笔和每盒笔芯的价格。
1.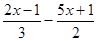 ≤1 2.
≤1 2.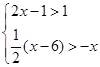
解方程组(1)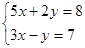
(2)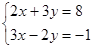
(3)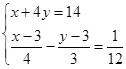
(4)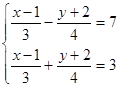
下图是行列间隔都为1个单位的点阵:
①你能计算点阵中多边形的面积吗?请将答案直接填入图中横线上。
②若用a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,你能用含a和b的代数式表示S= ____________________
③请你利用②中的公式来求a=4,b=20时,多边形的面积S。
(本题8分)已知有理数 满足①
满足① ;②
;② 是一个三次单项式且系数为-1:
是一个三次单项式且系数为-1:
(1)求 的值; (2)求代数式
的值; (2)求代数式 的值.
的值.
(本题7分)“十、一”黄金周期间,园博苑在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
| 日期 |
10月1日 |
10月2日 |
10月3日 |
10月4日 |
10月5日 |
10月6日 |
10月7日 |
| 人数变化 单位:千人 |
+1.6 |
+0.8 |
+0.4 |
-0.4 |
-0.8 |
+0.2 |
-1.2 |
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)若9月30日的游客人数为5千人,门票每人60元.问黄金周期间园博苑门票收入是多少元?