根据某研究院公布的2009~2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
| 年份 |
年人均阅读图书数量(本) |
| 2009 |
 |
| 2010 |
 |
| 2011 |
 |
| 2012 |
 |
| 2013 |
 |

根据以上信息解答下列问题:
(1)直接写出扇形统计图中 的值;
的值;
(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为 本;
(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为 本.
已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
|
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.

比较 与 的大小.
(1)尝试(用“ ”,“ ”或“ ”填空)
①当 时, ;
②当 时, ;
③当 时, .
(2)归纳:若 取任意实数, 与 有怎样的大小关系?试说明理由.
(1)计算: ;
(2)化简: .
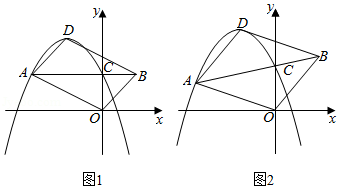
如图,已知在平面直角坐标系 中,抛物线 的顶点为 ,与 轴的交点为 .过点 的直线 与抛物线交于另一点 (点 在对称轴左侧),点 在 的延长线上,连结 , , 和 .
(1)如图1,当 轴时,
①已知点 的坐标是 ,求抛物线的解析式;
②若四边形 是平行四边形,求证: .
(2)如图2,若 , ,是否存在这样的点 ,使四边形 是平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.
已知在 中, , 是 边上的一点,将 沿着过点 的直线折叠,使点 落在 边的点 处(不与点 , 重合),折痕交 边于点 .
(1)特例感知 如图1,若 , 是 的中点,求证: ;
(2)变式求异 如图2,若 , , ,过点 作 于点 ,求 和 的长;
(3)化归探究 如图3,若 , ,且当 时,存在两次不同的折叠,使点 落在 边上两个不同的位置,请直接写出 的取值范围.
