对某一个函数给出如下定义：若存在实数
，对于任意的函数值
，都满足
，则称这个函数是有界函数，在所有满足条件的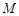
中，其最小值称为这个函数的边界值．例如，下图中的函数是有界函数，其边界值是1．
（1）分别判断函数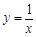
和
是不是有界函数？若是有界函数，求其边界值；
（2）若函数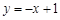
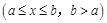的边界值是2，且这个函数的最大值也是2，求
的取值范围；
（3）将函数
的图象向下平移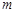
个单位，得到的函数的边界值是
，当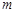在什么范围时，满足
？
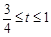图形的操作过程如下（本题中四个矩形的水平方向的边长均为a，竖直方向的边长均为b）在图①中，将线段A1A2向右平移1个单位长度到B1B2，得到封闭图形A1A2B2B1（即阴影部分）；在图②中，将折线A1A2A3（其中A2叫做折线A1A2A3的一个“折点”）向右平移1个单位长度到B1B2B3，得到封闭图形A1A2A2B3B2B1（即阴影部分）
（1）在图③中，请你类似地画一条有两个折点的折线，同样向右平移1个单位长度，从而得到一个封闭图形，并用斜线画出阴影部分．
（2）分别求出①，②，③三个图形中除去阴影部分后剩余部分的面积．
（3）联想与探索：如图④所示，在一块矩形草地上，有一条弯曲的柏油小路（小路的水平宽度是1个单位长度），请你猜想空白部分的草地面积是多少？并说明你的猜想是正确的．
某公司员工某月工资表如下：
| 员工 |
总经理 |
副经理 |
职员 A |
职员 B |
职员 C |
职员 D |
职员 E |
职员 F |
职员 G |
| 每月 工资（元） |
6000 |
3000 |
1200 |
1100 |
1700 |
1300 |
1100 |
500 |
1100 |
该公司三位职员对收入情况作出如下评价：
甲：我的月工资是1200元，在公司中算中等收入；
乙：我们好几个人的月工资都是1100元；
丙：我们公司员工收入很高，月工资为2000元．
请你用所学知识回答下列问题：（1）甲所说的数据1200元，我们称之为该组数据的；（填平均数、众数或中位数）
（2）乙所说的数据1100元，我们称之为该组数据的；（填平均数、众数或中位数）
（3）丙是用什么方法得出2000元的？
（4）甲、乙、丙三人的说法中，谁的说法可以较好地反映该公司职员收入的一般水平．
关于
的方程
有两个不相等的实数根（1）求
的取值范围；（2）是否存在实数
，使方程的两个实数根的倒数和等于0？若存在，求出的值；若不存在，请说明理由．
如图所示，已知△ABC是等边三角形，点D、F分别在线段BC，AB上，∠EFB=60º,DC=EF．
（1）求证：四边形EFCD是平行四边形；
（2）若BF=EF，求证AE=AD
由于自然灾害和人为破坏等因素，某地山林面积连续两年减少，现在的面积比两年前减少了36%，问平均每年减少的百分数是多少？