如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=4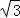
，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：
（1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．
（2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．
（3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．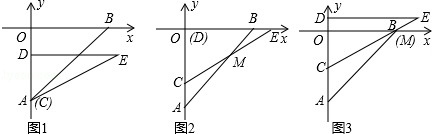
小明家刚买了新房，木匠师傅在为他家进行装修、如图，是一个四边形的木板边角料，小明通过测量，获得了如下数据：AB=4cm、AD=3cm、BC=12cm、CD=13cm，并且还知道BD⊥BC，小明由此认为这个四边形中∠A恰好是直角，你认为小明的判断正确吗？如果你认为他正确，请给出理由；如果你认为他不正确，请说明理由。
如图，在等腰梯形ABCD中，AD∥BC，对角线AC、BD相交于点O．
（1）图中共有对全等三角形；
（2）写出你认为全等的一对三角形，并给予说明理由。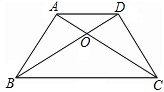
如图，△ABC是等边三角形， BD是中线，延长BC到点E，使CE＝CD.则DB和DE是否相等？为什么？
（3+3＝6分）已知△ABC，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法）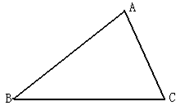
①作∠ABC的平分线BD交AC于点D；
②作线段BD的垂直平分线交AB于点E，交BC于点F。
由（1）、（2）可得：线段EF与线段BD的关系为：.
观察图的点阵图形和与之相对应的等式，探究其中的规律：
（1）请你在④和⑤后面的横线上分别写出相对应的等式；
（2）通过猜想，写出与第n个图形相对应的等式．