在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=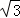 PC.(不必证明)
PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).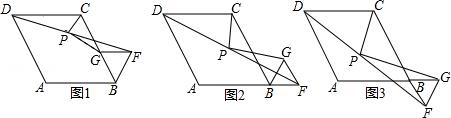
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当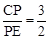 ,BP′=
,BP′=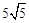 时,求线段AB的长.
时,求线段AB的长.
已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.
(1)求点M的坐标;
(2)求直线AB的解析式.
把分别标有数字2、3、4、5的四个小球放入A袋内,把分别标有数字 的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明。
的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明。
(1)小明分别从A、B两个袋子中各摸出一个小球,求这两个小球上的数字互为倒数的概率;
(2)当B袋中标有 的小球上的数字变为 时(填写所有结果),(1)中的概率为
的小球上的数字变为 时(填写所有结果),(1)中的概率为 。
。
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
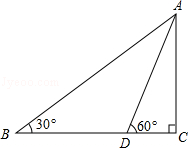
一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62米,到达D点,在测得山顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC(结果精确的1米,参考数值: )
)