如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
①∠AEF=∠BCE;
②AF+BC>CF;
③S△CEF=S△EAF+S△CBE;
④若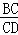 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.
其中正确的结论是 .(填写所有正确结论的序号)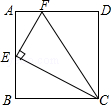
已知如图(1):△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.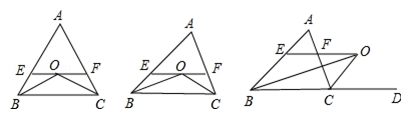
(1)写出线段EF与BE、CF间的数量关系?(不证明)
(2)若AB≠AC,其他条件不变,如图(2),图中线段EF与BE、CF间是否存在(1)中数量关系?请说明理由.
(3)若△ABC中,AB≠AC,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,如图(3),这时图中线段EF与BE,CF间存在什么数量关系?请说明理由.
常用的分解因式的方法有提取公因式法、公式法及十字相乘法,但有更多的多项式只用上述方法就无法分解,如x2﹣4y2﹣2x+4y,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为:x2﹣4y2﹣2x+4y=(x+2y)(x﹣2y)﹣2(x﹣2y)=(x﹣2y)(x+2y﹣2).
这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
(1)分解因式x2﹣2xy+y2﹣16;
(2)△ABC三边a,b,c 满足a2﹣ab﹣ac+bc=0,判断△ABC的形状.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.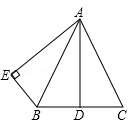
(1)求证:AD=AE.
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
(8分)甲乙两班学生参加了植树造林,已知甲班每天比乙班多植5棵,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等,求甲、乙班每天各植树多少棵?
8分)如图,在Rt△ABC中,∠C=90°,∠B=30°
(1)作边AB的垂直平分线交AB于点D,交BC于点E(尺规作图,不写作法,保留作图痕迹).
(2)连接AE,求证:AE=2DE.