如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．
（1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；
（2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？
（3）连接AF，在运动过程中，是否存在某一时刻t，使得S△AEF=
S四边形ABOF？若存在，请求出此时t的值；若不存在，请说明理由．
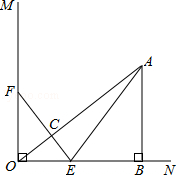
已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作菱形ADEF（A、D、E、F按逆时针排列），使∠DAF=60°，连接CF．
（1）如图1，当点D在边BC上时，求证：①BD=CF；②AC=CF+CD；
（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；
（3）如图3，当点D在边CB的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系．
如图，在⊙C的内接△AOB中，AB=AO=4，tan∠AOB=
，抛物线
（a≠0）经过点A（4，0）与点（﹣2，6）．
（1）求抛物线的解析式；
（2）直线m与⊙C相切于点A，交y轴于点D，动点P在线段OB上，从点O出发向点B运动，同时动点Q在线段DA上，从点D出发向点A运动，点P的速度为每秒1个单位长，点Q的速度为每秒2个单位长．当PQ⊥AD时，求运动时间t的值．
为提醒人们节约用水，及时修好漏水的水龙头．两名同学分别做了水龙头漏水实验，他们用于接水的量筒最大容量为100毫升．
实验一：小王同学在做水龙头漏水实验时，每隔10秒观察量筒中水的体积，记录的数据如表（漏出的水量精确到1毫升）：
| 时间t（秒） |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
| 漏出的水量V（毫升） |
2 |
5 |
8 |
11 |
14 |
17 |
20 |
（1）在图1的坐标系中描出上表中数据对应的点；
（2）如果小王同学继续实验，请探求多少秒后量筒中的水会满而溢出（精确到1秒）？
（3）按此漏水速度，一小时会漏水 千克（精确到0.1千克）
实验二：
小李同学根据自己的实验数据画出的图象如图2所示，为什么图象中会出现与横轴“平行”的部分？
已知一个口袋中装有7个只有颜色不同、其它都相同的球，其中3个白球、4个黑球．
（1）求从中随机取出一个黑球的概率．
（2）若往口袋中再放入x个黑球，且从口袋中随机取出一个白球的概率是
，求代数式
的值．
如图1，已知A（3，0）、B（4，4）、原点O（0，0）在抛物线y=ax2+bx+c （a≠0）上．
（1）求抛物线的解析式．
（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个交点D，求m的值及点D的坐标．
（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P的坐标（点P、O、D分别与点N、O、B对应）