如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求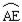 的长.
的长.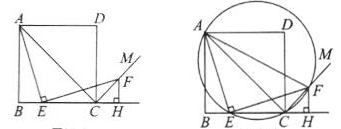
图1 图2
萧山素以“萝卜干之乡”著称.某乡组织20辆汽车装运A、B、C三种不同包装的萝卜干42吨到外地销售.按规定每辆车只装同一种萝卜干,且必须装满,每种萝卜干不少于2车.
设有x辆车装运A种萝卜干,用y辆车装运B种萝卜干,根据下表提供的信息,求y与x之间的函数关系,并求x的取值范围;
设此次外销活动的利润为W(百元),求W与x的函数关系式以及最大利润,并安排相应的车辆分配方案.
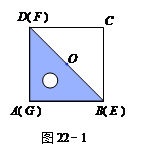
如图22-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.如图22-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
若三角尺GEF旋转到如图22-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.


问题背景:在 中,
中, 、
、 、
、 三边的长分别为
三边的长分别为 、
、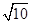 、
、 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点 (即
(即 三个顶点都在小正方形的顶点处),如图
三个顶点都在小正方形的顶点处),如图 所示.这样不需求
所示.这样不需求 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.请你将
 的面积直接填写在横线上.__________________
的面积直接填写在横线上.__________________
思维拓展:我们把上述求
 面积的方法叫做构图法.若
面积的方法叫做构图法.若 三边的长分别为
三边的长分别为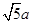 、
、 、
、 (
(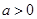 ),请利用图
),请利用图 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为 )画出相应的
)画出相应的 ,并求出它的面积.
,并求出它的面积.
探索创新:若
 三边的长分别为
三边的长分别为 、
、 、
、 (
( ,且
,且 ),试运用构图法求出这三角形的面积.
),试运用构图法求出这三角形的面积.
某校学生会准备调查2011级初三同学每天(除课间操外)的课外锻炼时间. 确定调查方式时,甲同学说:“我到(1)班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到2011级初三每个班去随机调查一定数量的同学”.请你指出哪位同学的调查方式最为合理;
他们采用了最为合理的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将条形统计图补充完整,并在扇形统计图中涂出一块表示“基本不参加”的部分;
若该校2011级初三共有420名同学,请你估计其中每天(除课间操外)课外锻炼时间不超过20分钟的人数.(注:图2中相邻两虚线形成的圆心角均为30°)

观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作 AD⊥BC于D(如图),则sinB= ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .同理有:
.同理有: ,
, ,所以
,所以
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.如图,△ABC中,∠B=450,∠C=750,BC=60,则∠A=;AC=;
如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.

