问题背景：在
中，
、
、
三边的长分别为
、
、
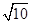，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图
所示．这样不需求的高，而借用网格就能计算出它的面积．请你将
的面积直接填写在横线上．__________________
思维拓展：我们把上述求
面积的方法叫做构图法．若三边的长分别为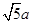
、
、
（
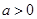），请利用图
的正方形网格（每个小正方形的边长为
）画出相应的，并求出它的面积．
探索创新：若
三边的长分别为
、
、
（
，且
），试运用构图法求出这三角形的面积．
计算：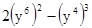
；
如图在下面直角坐标系中，已知A（0,a）,B（b,0）,C（3,c）三点，其中a、b、c满足关系式:
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（m，
），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积为△AOP的面积的两倍？若存在，求出点P的坐标，若不存在，请说明理由．
小文在甲、乙两家超市发现他看中的篮球的单价相同，书包单价也相同，一个篮球和三个书包的总费用是400元.两个篮球和一个书包的总费用也是400元.
（1）求小文看中的篮球和书包单价各是多少元？
（2）某一天小文上街，恰好赶上商家促销，超市甲所有商品打九折销售，超市乙全场购物满100元返30元购物券（不足100元不返券，购物券全场通用），如果他只能在同一家超市购买他看中的篮球和书包各一个，应选择哪一家超市购买更省钱？
暑假期间，学校布置了综合实践活动任务，王涛小组四人负责调查本村的500户农民的家庭收入情况，他们随机调查了40户居民家庭的收入情况（收入取整数，单位：元），并制定了频数分布表（如图Ⅰ）和频数分布直方图（如图Ⅱ）．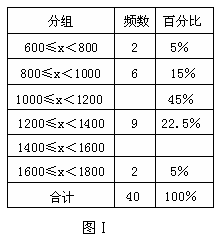
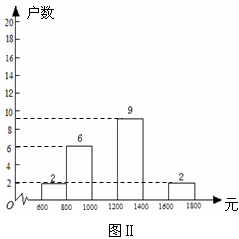
根据以上提供的信息，解答下列问题：
（1）补全频数分布表；
（2）补全频数分布直方图；
（3）请你估计该村属于中等收入（不低于1000元小于1600元）的大约有多少户?
方格纸中每个小方格都是边长为1个单位长度的正方形，在平面直角坐标系中，已知点A（－4，3）、B（－2，－3）.
（1）描出A、B两点的位置，并连结AB、AO、BO；
（2）△AOB的面积是__________；
（3）把△AOB向右平移4个单位，再向上平移2个单位得到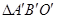
，在图中画出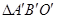，并写出点
、
、
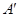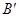的坐标.