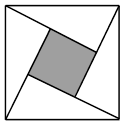
(本题8分)教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为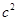 ,也可以表示为4×
,也可以表示为4×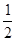 ab+
ab+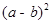 由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则
由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则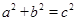 .
.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
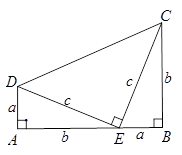
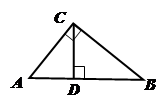
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为 cm.
|
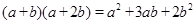 ,画在下面的网格中,并标出字母a、b所表示的线段.
,画在下面的网格中,并标出字母a、b所表示的线段.
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。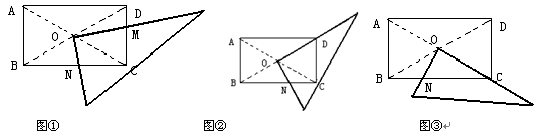
⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。
⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系(不需要证明)
已知:在四边形ABCD中,AC = BD,AC与BD交于点O,∠DOC = 60°.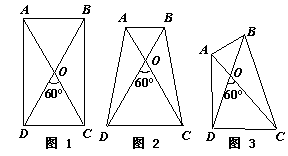
(1)当四边形ABCD是平行四边形时(如图1),证明AB + CD = AC;
(2)当四边形ABCD是梯形时(如图2),AB∥CD,线段AB、CD和线段AC之间的数量关系是_____________________________;
(3)如图3,四边形ABCD中,AB与CD不平行,结论AB + CD = AC是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
如图,任意四边形ABCD,对角线AC、BD交于O点,过各顶点分别作对角线AC、BD的平行线,四条平行线围成一个四边形EFGH.试想当四边形ABCD的形状发生改变时,四边形EFGH的形状会有哪些变化?完成以下题目: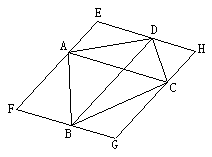
(1)当ABCD为任意四边形时,EFGH为________________;
当ABCD为矩形时,EFGH为________________;
当ABCD为菱形时,EFGH为________________;
当ABCD为正方形时,EFGH为________________;
当EFGH是矩形时,ABCD为________________;
当EFGH是菱形时,ABCD为________________;
当EFGH是正方形时,ABCD为________________.
(2)请选择(1)中任意一个你所写的结论进行证明.
(3)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件?
如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米 的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?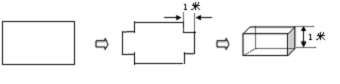
P、Q、R、S四个小球分别从正方形ABCD的四个定点A、B、C、D点出发,以同样的速度分别沿AB、BC、CD、DA的方向滚动,其终点分别是B、C、D、A。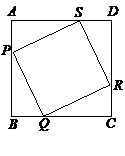
(1)不管滚动多长时间,求证:四边形PQRS为正方形;
(2)连结对角线AC、BD、PR、SQ,你发现四条对角线有何关系?
(3)根据此图,若有四个全等的直角三角形,你能否拼成一个正方形?若这个三角形直角边为a、b,斜边问c,你能否根据面积推导出勾股定理?