某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。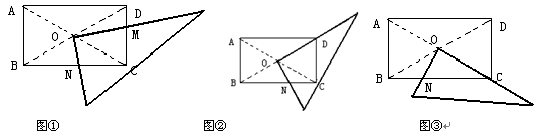
⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。
⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)
如图,在方格纸中,点C在直线AB外.
(1)请过C点画AB的垂线;
(2)过C点画AB的平行线CH;
(3)通过你的观察,直接写出CH与CB的位置关系.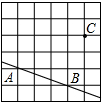
判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)等角的余角相等;
(2)平行线的同旁内角的平分线互相垂直;
(3)和为180°的两个角叫做邻补角.
用几何符号语言表示“互为邻补角的平分线互相垂直”的题设与结论,并画出图形.
试写出命题“两条直线相交,只有一个交点”的题设部分和结论部分.判断它是真命题还是假命题,并简要说明理由.
将下列命题改写成“如果…那么…”的形式.
(1)同位角相等,两直线平行;
(2)在同一平面内,垂直于同一直线的两直线平行.