娄底到长沙的距离约为180km，小刘开着小轿车，小张开着大货车，都从娄底去长沙，小刘比张晚出发1小时，最后两车同时到达长沙，已知小轿车的速度是大货车速度的1.5倍．
（1）求小轿车和大货车的速度各是多少？（列方程解答）
（2）当小刘出发时，求小张离长沙还有多远？
关于x的不等式组
无解，求a的取值范围
解方程组或不等式（组） （每题6分共30分）
（2）
（3）
（1）
（4）
（5）
如图，AB∥CD，分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系，请你从所得到的关系中任选一个加以说明。（适当添加辅助线，其实并不难）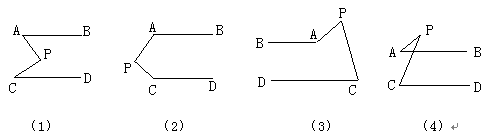
如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，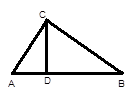
求：（1）△ABC的面积；
（2）CD的长；
（3）作出△ABC的边AC上的中线BE，并求出△ABE的面积；
（4）作出△BCD的边BC边上的高DF，当BD="11cm" 时，试求出DF的长。
如图，建立平面直角坐标系，使B，C的坐标分别为（－2，0）和（2，0）．
（1）画出坐标系，写出点A、D的坐标；
（2）若将△ABE向右平移4个单位，然后向上平移3个
单位后，得△A′B′E′，在图中画出△A′B′E′。