如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由.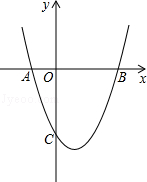
一次函数 的图象经过点 , .
(1)求该一次函数的解析式;
(2)若该一次函数的图象与反比例函数 的图象相交于 , , , 两点,且 ,求 的值.
某出租汽车公司计划购买 型和 型两种节能汽车,若购买 型汽车4辆, 型汽车7辆,共需310万元;若购买 型汽车10辆, 型汽车15辆,共需700万元.
(1) 型和 型汽车每辆的价格分别是多少万元?
(2)该公司计划购买 型和 型两种汽车共10辆,费用不超过285万元,且 型汽车的数量少于 型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.
某市气象局统计了5月1日至8日中午12时的气温(单位: ,整理后分别绘制成如图所示的两幅统计图.
根据图中给出的信息,解答下列问题:

(1)该市5月1日至8日中午时气温的平均数是 ,中位数是 ;
(2)求扇形统计图中扇形 的圆心角的度数;
(3)现从该市5月1日至5日的5天中,随机抽取2天,求恰好抽到2天中午12时的气温均低于 的概率.
化简: .
如图, , 和 相交于点 , .求证: .