某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.
(1)在点P运动时,这两个正方形面积之和是定值吗?如果时求出;若不是,求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点A,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.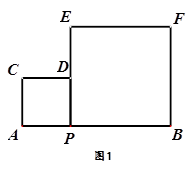
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向D点运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长。
(4)如图(3),在“问题思考”中,若点M、N是线段AB上的两点,且AM=BM=1,点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.

不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为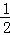 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
()如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.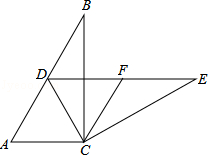
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?
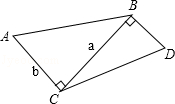
如图,已知∠ACB=∠CBD=90°,AC=b,CB=a,当BD与a,b之间满足怎样的关系时,△ACB∽△CBD?