()如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.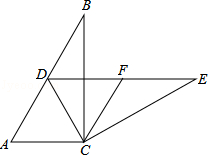
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.若翻到的纸牌是笑脸就有奖,小芳得奖的概率是多少?
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.小明认为这样得奖的概率是(1)中小芳得奖概率的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
如图,在△ABC与△ABD中,BC与AD相交于点O,∠1=∠2,CO=DO.求证:∠C=∠D.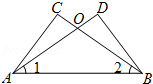
解分式方程: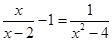 .
.
已知a2-2a-3=0,求代数式2a(a-1)-(a+2)(a-2)的值.
将长为20cm,宽为10cm的长方形白纸,按如图所示的方法粘贴起来,粘合部分的宽为2cm.设x张白纸粘合后的纸条总长度为ycm,
(1)求y与x之间的函数关系式,并画出函数图象,
(2)若x=20,求纸条的面积.