某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.若翻到的纸牌是笑脸就有奖,小芳得奖的概率是多少?
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.小明认为这样得奖的概率是(1)中小芳得奖概率的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
(本小题满分12分)如图所示,在梯形 中,
中, ,
, ,以
,以 为直径的
为直径的 与
与 相切于
相切于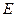 .已知
.已知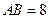 ,边
,边 比
比 大6.
大6.
(1)求边 、
、 的长.
的长.
(2)在直径 上是否存在一动点
上是否存在一动点 ,使以
,使以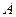 、
、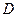 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(本小题满分10分)一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个.若从中任意摸出一个球,这个球是白球的概率为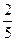 .
.
(1)求口袋中红球的个数;
(2)把口袋中的球搅匀后摸出一个球,放回搅匀再摸出第二个球,求摸到的两个球是一红一白的概率.(请结合树状图或列表加以解答)
(本小题满分10分)如图,已知反比例函数 (
( )的图象与一次函数
)的图象与一次函数 的图象交于
的图象交于 两点,点
两点,点 的坐标为
的坐标为 ,连接
,连接 平行于
平行于 轴.
轴.
(1)求反比例函数的解析式及点 的坐标.
的坐标.
(2)现有一个直角三角板,让它的直角顶点 在反比例函数图象上的
在反比例函数图象上的 之间的部分滑动(不与
之间的部分滑动(不与 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于 轴、
轴、 轴,且与线段
轴,且与线段 交于
交于 两点,试判断
两点,试判断 点在滑动过程中
点在滑动过程中 是否与
是否与 总相似,简要说明判断理由.
总相似,简要说明判断理由.
(本小题满分8分)
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
 |
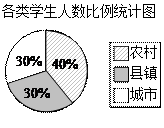
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
(本小题满分8分)
如图,在菱形 中,
中,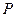 是
是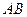 上的一个动点(不与
上的一个动点(不与 重合),连接
重合),连接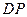 交对角线
交对角线 于
于 ,连接
,连接 .
.
(1)求证: ;
;
(2)若 ,试问
,试问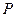 点运动到什么位置时
点运动到什么位置时 的面积等于菱形
的面积等于菱形 面积的
面积的 ?为什么?
?为什么?