某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与 元成反比例.又当
元成反比例.又当 时,
时,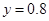 .
.
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益 用电量
用电量 (实际电价-成本价)]
(实际电价-成本价)]
如图,在四棱锥P-ABCD中,底面为直角梯形, 垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求点B到平面PAC的距离.
对某校高一年级学生参加社区服务次数进行统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数的统计如下:
| 分组 |
频数 |
频率 |
| [10,15) |
9 |
0.45 |
| [15,20) |
5 |
n |
| [20,25) |
m |
r |
| [25,30) |
2 |
0.1 |
| 合计 |
M |
1 |
(Ⅰ)求出表中M,r,m,n的值;
(Ⅱ)在所取样本中,从参加社区服务次数不少于20次的学生中任选2人,求至少有1人参加社区服务次数在区间[25,30)内的概率.
在 中,
中, 分别为角
分别为角 的对边,
的对边, 的面积
的面积 满足
满足 .
.
(Ⅰ)求角A的值;
(Ⅱ)若 ,设角B的大小为x,用x表示c并求的取值范围.
,设角B的大小为x,用x表示c并求的取值范围.
设数列 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为 ,对于任意正整数m,n,
,对于任意正整数m,n,  恒成立.
恒成立.
(Ⅰ)若 =1,求
=1,求 及数列
及数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求证:数列
,求证:数列 是等比数列.
是等比数列.
设函数 ;
;
(Ⅰ)求证:函数 在
在 上单调递增;
上单调递增;
(Ⅱ)设 ,若直线PQ∥x轴,求P,Q两点间的最短距离.
,若直线PQ∥x轴,求P,Q两点间的最短距离.