设二次函数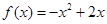 .
.
(1)求函数 的最小值;
的最小值;
(2)问是否存在这样的正数 ,当
,当 时,
时,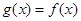 ,且
,且 的值域为
的值域为 ?若存在,求出所有的
?若存在,求出所有的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分12分)如图,四棱锥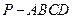 中,底面
中,底面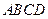 为平行四边形,
为平行四边形,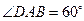 ,
,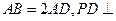 底面
底面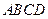 .
.
(1)证明: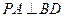 ;
;
(2)若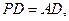 求二面角
求二面角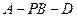 的余弦值.
的余弦值.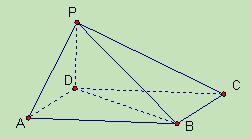
(本小题满分12分)如图,已知圆心坐标为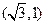 的圆
的圆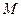 与
与 轴及直线
轴及直线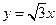 分别相切于
分别相切于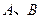 两点,另一圆
两点,另一圆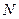 与圆
与圆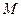 外切,且与
外切,且与 轴及直线
轴及直线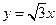 分别相切于
分别相切于 两点.
两点.
(1)求圆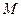 和圆
和圆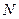 的方程;(2)过点
的方程;(2)过点 作直线
作直线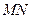 的平行线
的平行线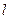 ,求直线
,求直线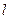 被圆
被圆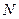 截得的弦的长度.
截得的弦的长度.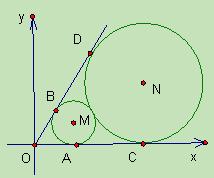
(本小题满分12分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用).已建仓库的底面直径为12m,高4m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(底面面积不计);
(3)哪个方案更经济些?
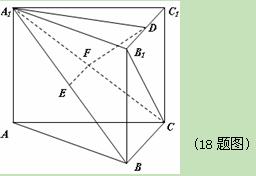
(本小题满分12分)如图,在直三棱柱 中,
中, 、
、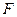 分别是
分别是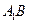 、
、 的中点,点
的中点,点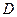 在
在 上,
上,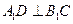 。
。
求证:(1)EF∥平面ABC;
(2)平面
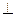 平面
平面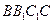 .
.
(本小题满分10分)已知直线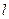 的斜率为
的斜率为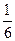 ,且和坐标轴围成面积为3的三角形,求直线
,且和坐标轴围成面积为3的三角形,求直线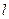 的方程。
的方程。