如图,在梯形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAD的平分线AE交BC于E,G是AD的中点,连接DE.
(1)猜想四边形ABED的形状,并说明理由;
(2)当AB与EC满足怎样的数量关系时,EG∥CD?并说明理由.
图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象。根据图象回答问题:
在这个变化过程中,自变量是____,因变量是______。
9时,10时30分,12时所走的路程分别是多少?
他休息了多长时间?
他从休息后直至到达目的地这段时间的平均速度是多少?
火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x、y、z的箱子按如图所示的方式打包,则打包带的长至少为多少?
在下面的解题过程的横线上填空,并在括号内注明理由
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
长方形纸片的长是15㎝,长宽上各剪去两个宽为3㎝的长条,剩下的面积是原面积的 ,求原长方形的宽。
,求原长方形的宽。
已知:线段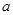 、
、 和∠β(如图),利用直尺和圆规作ΔABC,使BC=
和∠β(如图),利用直尺和圆规作ΔABC,使BC=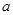 ,AB=
,AB= ,∠ABC=∠β。(不写作法,保留作图痕迹)。
,∠ABC=∠β。(不写作法,保留作图痕迹)。
