将数列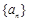
中的所有项按每一行比上一行多两项的规则排成如下数表：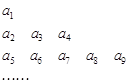
已知表中的第一列数
构成一个等差数列, 记为
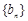, 且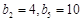
, 表中每一行正中间一个数
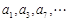构成数列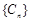
, 其前n项和为
.
(1)求数列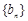的通项公式；(2)若上表中, 从第二行起, 每一行中的数按从左到右的顺序均构成等比数列, 公比为同一个正数, 且
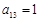.①求；②记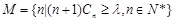
, 若集合M的元素个数为3, 求实数
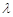的取值范围.
单调函数f(x)满足f(x + y)= f(x) + f(y)，且f(1)=2，其定义域为R。
(1)求f(0)、f(2)、f(4)的值； (2)解不等式f(x2+ 3 x) < 8。
如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形，|AM|=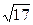
，|AN|=3，且|BN|=6.建立适当的坐标系，求曲线段C的方程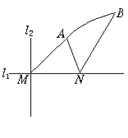
双曲线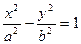
(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(－1,0)到直线l的距离之和s≥
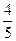c.求双曲线的离心率e的取值范围．
如图椭圆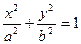
(a>b>0)的上顶点为A，左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上．
（1）求椭圆的离心率；
（2）若平行四边形OCED的面积为
, 求椭圆方程．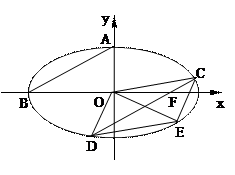
已知复数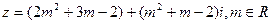
根据下列条件，求m值．
（1）z是实数；（2）z是虚线；（3）z是纯虚数；（4）z＝0．