某花店经营部每天的房租，人员工资等固定成本为150元，每盆花进价5元，销售单价与日均销售量的关系如下表:
| 销售单价/元 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 日均销量/盆 |
500 |
460 |
420 |
380 |
340 |
300 |
260 |
请根据数据分析，这个经营部怎样定价才能获得最大利润.
（14 分）如图（1）是一正方体的表面展开图，MN 和PB 是两条面对角线，请在图（2）的正方体中将MN 和PB 画出来，并就这个正方体解决下面问题。
（1）求证：MN//平面PBD；
（2）求证：AQ⊥平面PBD；
（3）求二面角P—DB—M 的大小．
（14 分）已知函数
的最大值为1．
（1）求常数a 的值；
（2）求
的单调递增区间；
（3）求≥ 0 成立的x 的取值集合．
已知椭圆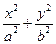
（a＞b＞0）的离心率
，过点A（0，-b）和B（a，0）的直线与原点的距离为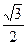
．
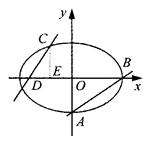
（1）求椭圆的方程．
（2）已知定点E（-1，0），若直线y＝kx＋2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由．
双曲线
(a>0,b>0)满足如下条件:(1) ab=
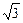;(2)过右焦点F的直线l的斜率为
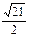，交y轴于点P，线段PF交双曲线于点Q，且|PQ|:|QF|=2:1,求双曲线的方程.
已知椭圆
,P为该椭圆上一点.
(1)若P到左焦点的距离为3,求到右准线的距离；
(2)如果F1为左焦点,F2为右焦点,并且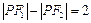
,求
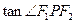的值