如图所示，在第一、二象限存在场强均为E的匀强电场，其中第一象限的匀强电场的方向沿x轴正方向，第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场，矩形区域的AB边与x轴重合。M是第一象限中无限靠近y轴的一点，在M点有一质量为m、电荷量为e的质子，以初速度v0沿y轴负方向开始运动，恰好从N点进入磁场，若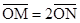
，不计质子的重力，试求：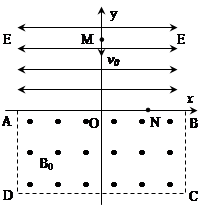
（1）N点横坐标d；
（2）若质子经过磁场最后能无限靠近M点，则矩形区域的最小面积是多少；
（3）在（2）的前提下，该质子由M点出发返回到无限靠近M点所需的时间。
如图（a）所示，木板OA可绕轴O在竖直平面内转动，某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F＝8N的力作用下加速度与斜面倾角的关系。已知物块的质量m＝1kg，通过DIS实验，得到如图（b）所示的加速度与斜面倾角的关系图线。若物块与木板间的动摩擦因数为0.2，假定物块与木板间的最大静摩擦力始终等于滑动摩擦力，g取10m/s2。试问：
（1）图（b）中图线与纵坐标交点ao多大？
（2）图（b）中图线与θ轴交点坐标分别为θ1和θ2，木板处于该两个角度时的摩擦力指向何方？说明在斜面倾角处于θ1和θ2之间时物块的运动状态。
（3）θ1为多大？
（4）如果木板长L＝2m，倾角为37°，物块在F的作用下由O点开始运动，为保证物块不冲出木板顶端，力F最多作用多长时间？（取sin37°＝0.6，cos37°＝0.8）
如图所示，电荷量均为＋q、质量分别为m和2m的小球A和B，中间连接质量不计的细绳，在竖直方向的匀强电场中以速度v0匀速上升，某时刻细绳突然断开．求：
(1)电场强度大小及细绳断开后两球A、B的加速度；
(2)当球B速度为零时，球A的速度大小。
一半径为R的1/4球体放置在水平面上，球体由折射率为
的透明材料制成。现有一束位于过球心O的竖直平面内的光线，平行于桌面射到球体表面上，折射入球体后再从竖直表面射出，如图所示。已知入射光线与桌面的距离为
。求出射角
。
一气象探测气球，在充有压强为1.00atm（即76.0cmHg）、温度为27.0℃的氦气时，体积为3.50m3。在上升至海拔6.50km高空的过程中，气球内氦气压强逐渐减小到此高度上的大气压36.0cmHg，气球内部因启动一持续加热过程而维持其温度不变。此后停止加热，保持高度不变。已知在这一海拔高度气温为-48.0℃。求：
①氦气在停止加热前的体积；
②氦气在停止加热较长一段时间后的体积。
如右图所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中，A2A4与A1A3的夹角为60°。一质量为m，带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场，随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区，最后再从A4处射出磁场。已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中的磁感应强度的大小。（忽略粒子重力）。