某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| |
有关系 |
无关系 |
不知道 |
| 40岁以下 |
800 |
450 |
200 |
| 40岁以上(含40岁) |
100 |
150 |
300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从持有关系态度的人中抽取45人,求n的值.
(2)在持“不知道”态度的人中,用分层抽样的方法抽取10人看作一个总体.①从这10人中选取3人,求至少一人在40岁以下的概率;②从这10人中人选取3人,若设40岁以下的人数为X,求X的分布列和数学期望.
(本小题12分)已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数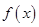 的解析式,并写出
的解析式,并写出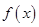 的单调减区间;
的单调减区间;
(2)已知 的内角分别是
的内角分别是 ,角
,角 为锐角,且
为锐角,且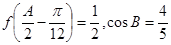 ,求
,求 的值.
的值.
(本小题10分)已知数列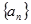 是公比不为
是公比不为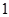 的等比数列,
的等比数列, ,且
,且 成等差数列.
成等差数列.
(1)求数列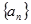 的通项;
的通项;
(2)若数列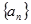 的前
的前 项和为
项和为 ,试求
,试求 的最大值.
的最大值.
(本小题12分)已知函数 .
.
(1)若 =0,判断函数
=0,判断函数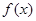 的单调性;
的单调性;
(2)若 时,
时,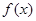 <0恒成立,求
<0恒成立,求 的取值范围.
的取值范围.
(本小题12分)过椭圆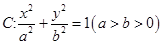 右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为 .
.
(1)求椭圆C的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点P,Q,且 ⊥
⊥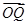 ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
(本小题12分)如图,在四棱锥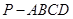 中,
中,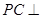 底面ABCD,底面ABCD是直角梯形,
底面ABCD,底面ABCD是直角梯形,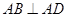 ,
, ,
,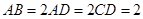 ,
,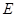 是
是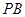 的中点
的中点
(1)求证:平面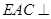 平面
平面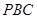 ;
;
(2)若二面角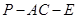 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.