设椭圆C: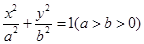
的离心率
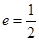，右焦点到直线
1的距离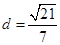
，O为坐标原点.
（1）求椭圆C的方程;
（2）过点O作两条互相垂直的射线，与椭圆C分别交于A、B两点，证明点O到直线AB的距离为定值，并求弦AB长度的最小值.
已知数列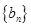
是首项为1，公差为2的等差数列，数列
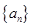的前n项和
．
(I)求数列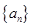的通项公式；
(II)设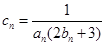
, 求数列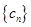
的前n项和
．
如图，四边形ABCD为正方形，PA
平面ABCD，且AD= 2PA，E、F、G、H分别是线段PA、PD、CD、BC的中点．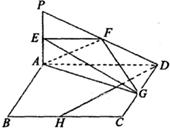
(I)求证：BC∥平面EFG；
(II)求证：DH平面AEG．
已知函数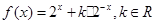
.
(I)若函数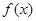
为奇函数，求实数
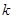的值；
(II)若对任意的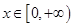
，都有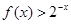
成立，求实数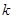的取值范围．
在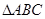
中，角A、B、C的对边分别为a、b、c，且角A、B、C成等差教列．
(I)若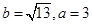
，求边c的值；
(II)设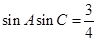
，求角A的最大值．
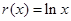已知函数
，函数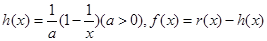
．
(I)试求f(x)的单调区间。
(II)若f(x)在区间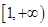
上是单调递增函数，试求实数a的取值范围：
(III)设数列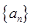
是公差为1．首项为l的等差数列，数列
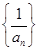的前n项和为
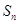，求证：当
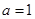时，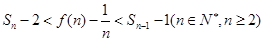
.