如图，已知二次函数的图象过点O（0，0），A（4，0），B（2，﹣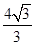
），M是OA的中点．
（1）求此二次函数的解析式；
（2）设P是抛物线上的一点，过P作x轴的平行线与抛物线交于另一点Q，要使四边形PQAM是菱形，求P点的坐标；
（3）将抛物线在x轴下方的部分沿x轴向上翻折，得曲线OB′A（B′为B关于x轴的对称点），在原抛物线x轴的上方部分取一点C，连接CM，CM与翻折后的曲线OB′A交于点D．若△CDA的面积是△MDA面积的2倍，这样的点C是否存在？若存在求出C点的坐标，若不存在，请说明理由．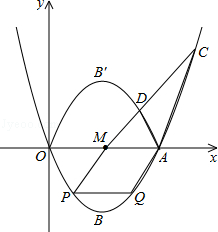
长方体甲的长宽高分别为260mm，150mm，325mm，长方体乙的地底面积为130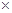
130mm2。已知甲的体积是乙的体积的2.5倍，求乙的高。
把一个长宽高分别为8cm，7cm，6cm的长方体铁块和一个棱长5cm正方体铁块，熔炼成一个直径为20cm的圆柱体，这个圆柱体的高是多少？（精确到0.01cm）
一捆粗细均匀的钢丝，重量为132kg，剪下35米后，余下的钢丝重量为121kg，求原来这根钢丝的长度。
要分别锻造直径70mm，高45mm和直径30mm，高30mm的圆柱形零件毛坯各一个，需要截取直径50mm的圆钢多长？
把直径6cm，长16cm的圆钢锻造成半径为4cm圆钢，求锻造后的圆钢的长。