如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.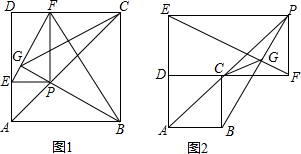
(本题12分)如图①所示,直线L: 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点。
轴正半轴分别交于A、B两点。
(1)当OA=OB时,试确定直线L的解析式;


(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,试说明MN=AM+BN。
(3)当 取不同的值时,点B在
取不同的值时,点B在 轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交
轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交 轴于P点,如图③。
轴于P点,如图③。
问:当点B在 y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由。
(本题12分)在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1) 直接写出甲骑自行车的速度;乙骑自行车的速度;
(2) 求出点M的坐标,并解释该点坐标所表示的实际意义;
(3) 若两人之间保持的距离不超过2km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
(本题12分)已知:如图1,点D是边长为2的等边△ABC边BC所在直线上的一动点,从点B向C方向运动,以AD为边向右侧作等边△ADE。
(1)连接CE,若点D在边BC上时,易知线段CE 、CD、AC三者之间的关系为CE+CD="AC;" 如图2当点D在C的右侧时,试探索线段CE 、CD、AC三者之间的数量关系,并说明理由。
(2如图1,当点D从B运动到C时,①直接写出△CDE周长的最小值。②直接写出点E的运动路径长。
(3)若将题目中条件“等边△ADE”改为“满足∠ADE=60°与等边△ABC的外角平分线交于点E”,那么CE与BD还相等吗?如图3请作出判断并给出说明。


图1图2图3
(本题10分)某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有甲、乙两家印刷社,制作此种宣传单的收费标准如下:
甲印刷社收费y(元)与印制数x(张)的函数关系如下表:
| 印制x(张) |
… |
100 |
200 |
300 |
… |
| 收费y(元) |
… |
15 |
30 |
45 |
… |
乙印刷社的收费方式为:500张以内(含500张),按每张0.20元收费;超过500张部分,按每张0.10元收费.
(1)根据表中规律,写出甲印刷社收费y(元)与印数x(张)的函数关系式;
(2)兴趣小组决定制作宣传单(已知印数超过500张),若在甲、乙印刷社中选一家,兴趣小组应选择哪家印刷社比较划算?并说明理由。
(本题10分)已知:如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.CM⊥AE,垂足是F, 交AD于N,交AB于M,连接ME。
(1)求证:ME⊥BC;
(2)若AB= ,试求ME的长。
,试求ME的长。