(本题12分)已知:如图1,点D是边长为2的等边△ABC边BC所在直线上的一动点,从点B向C方向运动,以AD为边向右侧作等边△ADE。
(1)连接CE,若点D在边BC上时,易知线段CE 、CD、AC三者之间的关系为CE+CD="AC;" 如图2当点D在C的右侧时,试探索线段CE 、CD、AC三者之间的数量关系,并说明理由。
(2如图1,当点D从B运动到C时,①直接写出△CDE周长的最小值。②直接写出点E的运动路径长。
(3)若将题目中条件“等边△ADE”改为“满足∠ADE=60°与等边△ABC的外角平分线交于点E”,那么CE与BD还相等吗?如图3请作出判断并给出说明。


图1 图2 图3
如图,方格纸上每个小正方形的边长均为1个单位长度,点 、 都在格点上(两条网格线的交点叫格点).
(1)将线段 向上平移两个单位长度,点 的对应点为点 ,点 的对应点为点 ,请画出平移后的线段 ;
(2)将线段 绕点 按逆时针方向旋转 ,点 的对应点为点 ,请画出旋转后的线段 ;
(3)连接 、 ,求 的面积.

某企业为了解员工安全生产知识掌握情况,随机抽取了部分员工进行安全生产知识测试,测试试卷满分100分.测试成绩按 、 、 、 四个等级进行统计,并将统计结果绘制了如下两幅不完整的统计图.(说明:测试成绩取整数, 级:90分 分; 级:75分 分; 级:60分 分; 级:60分以下)
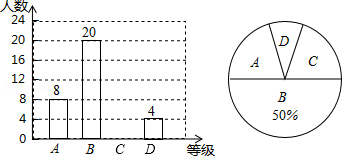
请解答下列问题:
(1)该企业员工中参加本次安全生产知识测试共有 人;
(2)补全条形统计图;
(3)若该企业共有员工800人,试估计该企业员工中对安全生产知识的掌握能达到 级的人数.
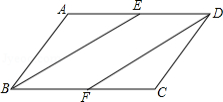
已知:如图,在 中,点 、 分别是边 、 的中点.求证: .
已知平面图形 ,点 、 是 上任意两点,我们把线段 的长度的最大值称为平面图形 的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .
①若 ,用直尺和圆规画出点 所在的区域并求它的面积(所在区域用阴影表示);
②若点 在 上运动, 的半径为1,圆心 在过点 且与 轴垂直的直线上.对于 上任意点 ,都有 ,直接写出圆心 的横坐标 的取值范围.

如图,二次函数 的图象与 轴交于点 、 ,与 轴交于点 ,点 的坐标为 ,点 为 的中点,点 在抛物线上.
(1) ;
(2)若点 在第一象限,过点 作 轴,垂足为 , 与 、 分别交于点 、 .是否存在这样的点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由;
(3)若点 的横坐标小于3,过点 作 ,垂足为 ,直线 与 轴交于点 ,且 ,求点 的坐标.
