七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
| 月均用水量x(t) |
频数(户) |
百分比 |
| 0<x≤5 |
6 |
12% |
| 5<x≤10 |
|
24% |
| 10<x≤15 |
|
32% |
| 15<x≤20 |
10 |
20% |
| 20<x≤25 |
4 |
|
| 25<x≤30 |
2 |
4% |
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)本次随机调查了多少户家庭?若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)试判断线段BD与CD的大小关系;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)若△ABC为直角三角形,且∠BAC=90°时,判断四边形AFBD的形状,并说明理由.
淮北市2013年中招体育考试刚刚结束,为了了解某校九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:31分-35分;B级:26分-30分;C级:21分-25分;D级:21分以下)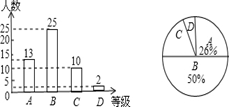
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图中C级所在的扇形圆心角的度数;
(3)该班学生体育测试成绩的中位数落在哪个等级内;
(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
据媒体报道,我国2010年公民出境旅游总人数约5000万人次,2012年公民出境旅游总人数约7200万人次,若2011年、2012年公民出境旅游总人数逐年递增,请解答下列问题:
(1)求这两年我国公民出境旅游总人数的年平均增长率;
(2)如果2012年仍保持相同的年平均增长率,请你预测2013年我国公民出境旅游总人数约多少万人次?
如图,西园中学数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点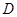 的仰角为
的仰角为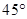 ,再沿着
,再沿着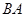 的方向后退20m至
的方向后退20m至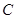 处,测得古塔顶端点
处,测得古塔顶端点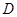 的仰角为
的仰角为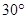 ,求该古塔BD的高度(
,求该古塔BD的高度(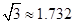 ,结果保留一位小数).
,结果保留一位小数).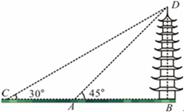
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使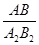 =
=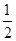 ,并写出点A2的坐标。
,并写出点A2的坐标。