如图,在平面直角坐标系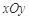 中,
中, 分别是椭圆
分别是椭圆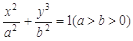 的左、右焦点,顶点
的左、右焦点,顶点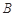 的坐标为
的坐标为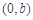 ,连结
,连结 并延长交椭圆于点A,过点A作
并延长交椭圆于点A,过点A作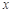 轴的垂线交椭圆于另一点C,连结
轴的垂线交椭圆于另一点C,连结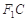 .
.
(1)若点C的坐标为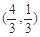 ,且
,且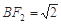 ,求椭圆的方程;
,求椭圆的方程;
(2)若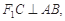 求椭圆离心率e的值.
求椭圆离心率e的值.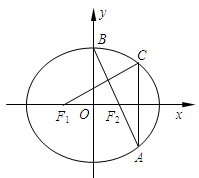
(本小题满分12分)已知函数 (I)求函数
(I)求函数 上的最小值;(II)求证:对一切
上的最小值;(II)求证:对一切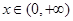 ,都有
,都有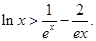
已知函数 =
=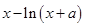 在
在 处取得极值.
处取得极值.
(1)求实数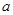 的值;
的值;
(2) 若关于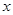 的方程
的方程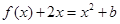 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
设数列 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,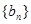 为等比数列,且
为等比数列,且
(Ⅰ)求数列 和
和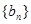 的通项公式;
的通项公式;
(Ⅱ)设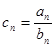 ,求数列
,求数列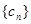 的前n项和Tn.
的前n项和Tn.
A、B是双曲线x2-=1上的两点,点N(1,2)是线段AB的中点
(1)求直线AB的方程;
(2)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点。
(1)求证:直线MF∥平面ABCD;
(2)求平面AFC1与平面ABCD所成二面角的大小。