设数列 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,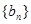 为等比数列,且
为等比数列,且
(Ⅰ)求数列 和
和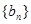 的通项公式;
的通项公式;
(Ⅱ)设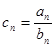 ,求数列
,求数列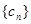 的前n项和Tn.
的前n项和Tn.
(本题满分10分) 选修4—5:不等式选讲
已知关于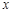 的不等式
的不等式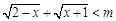 对于任意的
对于任意的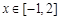 恒成立
恒成立
(Ⅰ)求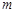 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下求函数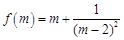 的最小值.
的最小值.
(本题满分10分) 选修4—4:极坐标与参数方程
在直角坐标平面内,以坐标原点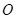 为极点,
为极点,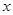 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 、
、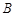 的极坐标分别为
的极坐标分别为 、
、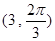 ,曲线
,曲线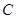 的参数方程为
的参数方程为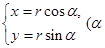 为参数).
为参数).
(Ⅰ)求直线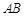 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线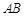 和曲线C只有一个交点,求
和曲线C只有一个交点,求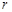 的值.
的值.
(本小题满分12分)已知函数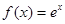
(Ⅰ)当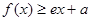 对任意的实数x恒成立,求a的取值范围;
对任意的实数x恒成立,求a的取值范围;
(Ⅱ)若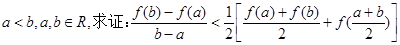 .
.
(本小题满分12分)如图,圆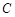 与
与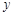 轴相切于点
轴相切于点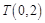 ,与
,与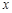 轴正半轴相交于两点
轴正半轴相交于两点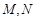 (点
(点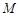 在点
在点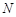 的左侧),且
的左侧),且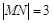 .
.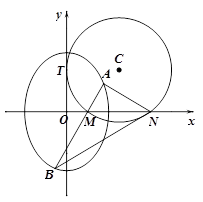
(Ⅰ)求圆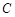 的方程;
的方程;
(Ⅱ)过点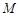 任作一条直线与椭圆
任作一条直线与椭圆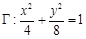 相交于两点
相交于两点 ,连接
,连接 ,求证:
,求证: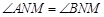 .
.
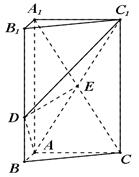
(本小题满分12分)如图,三棱柱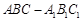 中,
中,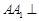 平面
平面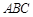 ,
,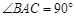 ,
,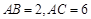 , 点
, 点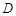 在线段
在线段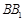 上,且
上,且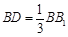 ,
,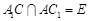 .
.
(Ⅰ)求证:直线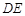 与平面
与平面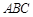 不平行;
不平行;
(Ⅱ)设平面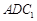 与平面
与平面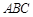 所成的锐二面角为
所成的锐二面角为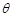 ,若
,若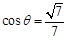 ,求
,求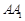 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面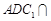 平面
平面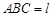 ,求直线
,求直线 与
与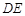 所成的角的余弦值.
所成的角的余弦值.