已知某工厂计划用库存的302m3木料为某学校生产500套桌椅,供该校1250名学生使用,该厂生产的桌椅分为A,B两种型号,有关数据如下:
| 桌椅型号 |
一套桌椅所坐学生人数(单位:人) |
生产一套桌椅所需木材(单位:m3) |
一套桌椅的生产成本(单位:元) |
一套桌椅的运费(单位:元) |
| A |
2 |
0.5 |
100 |
2 |
| B |
3 |
0.7 |
120 |
4 |
设生产A型桌椅x(套),生产全部桌椅并运往该校的总费用(总费用=生产成本+运费)为y元.
(1)求y与x之间的关系式,并指出x的取值范围;
(2)当总费用y最小时,求相应的x值及此时y的值.
如图,已知双曲线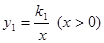 经过点M,它关于y轴对称的双曲线为
经过点M,它关于y轴对称的双曲线为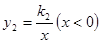 .
.
(1)求双曲线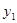 与
与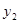 的解析式;
的解析式;
(2)若平行于 轴的直线交双曲线
轴的直线交双曲线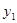 于点A,交双曲线
于点A,交双曲线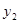 于点B,在
于点B,在 轴上存在点P,使以点A,B,O,P为顶点的四边形是菱形,求点P的坐标.
轴上存在点P,使以点A,B,O,P为顶点的四边形是菱形,求点P的坐标.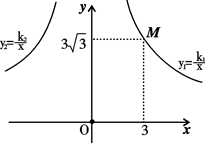
“兄弟餐厅”采购员某日到集贸市场采购草鱼,若当天草鱼的采购单价 (元)与采购量
(元)与采购量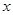 (斤)之间的关系如图,且采购单价不低于4元/斤.
(斤)之间的关系如图,且采购单价不低于4元/斤.
(1)直接写出 关于
关于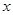 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)若这天他采购草鱼的量不多于20斤,那么这天他采购草鱼最多用去多少钱?
已知关于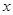 的方程
的方程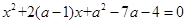 .
.
(1)若方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)若方程的两个实数根为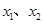 ,且满足
,且满足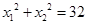 ,求
,求 的值.
的值.
某中学对全校学生1分钟跳绳的次数进行了统计,全校1分钟跳绳的平均次数是100次.某班体育委员统计了全班50名学生1分钟跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点).
(1)求该班学生中跳绳次数达到或超过校平均水平的占全班人数的百分比;
(2)该班1分钟跳绳的平均次数至少是多少?是否超过全校平均次数?
(3)已知该班成绩最好的三名学生中有一名男生和两名女生,现要从三人中随机抽取两人参加学校举行的跳绳比赛,用列表或画树状图的方法求恰好抽到一名男生和一名女生的概率.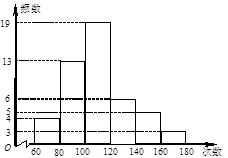
某企业向阳光小学赠送300个学生书包.现用A,B两种不同的包装箱进行包装,单独用B型包装箱比单独用A型包装箱少用10个,已知每个B型包装箱比每个A型包装箱多装5个书包.求A,B两种包装箱各能装书包多少个?