某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| |
空调 |
彩电 |
| 进价(元/台) |
5400 |
3500 |
| 售价(元/台) |
6100 |
3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
在一分钟投篮测试中,甲、乙两组同学的一次测试成绩如下:
| 成绩 |
4 |
5 |
6 |
7 |
8 |
9 |
| 甲组(人) |
1 |
2 |
4 |
2 |
1 |
5 |
| 乙组(人) |
1 |
1 |
3 |
5 |
2 |
3 |
(1)求甲、乙两组一分钟投篮测试成绩的平均数和方差;
(2)从统计学的角度看,你认为哪组同学的测试成绩较好?为什么?
如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
如图,在△ABC和△DCB中,AC与BD交于点E,且AC=BD,AB=CD.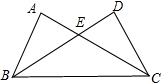
(1)求证:△ABC≌△DCB;(2)若∠AEB=70°,求∠EBC的度数.
先化简,再求值 ,其中
,其中 .
.
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.
(1)求证:△ACM≌△BCP;
(2)若PA=1,PB=2,求△PCM的面积.