在平面直角坐标系
中，二次函数
的图像与
轴交于点A，B（点B在点A的左侧），与
轴交于点C，过动点H（0, 
）作平行于轴的直线，直线与二次函数的图像相交于点D，E.
（1）写出点A,点B的坐标；
（2）若
，以DE为直径作⊙Q，当⊙Q与轴相切时，求的值；
（3）直线上是否存在一点F，使得△ACF是等腰直角三角形？若存在，求的值；若不存在，请说明理由.
如图，一艘核潜艇在海面下500米
点处测得俯角为
正前方的海底有黑匣子信号发出，继续在同一深度直线航行4000米后再次在
点处测得俯角为
正前方的海底有黑匣子信号发出，求海底黑匣子
点处距离海面的深度？（精确到米，参考数据：
，
，
）
（1）计算：
．
（2）解方程组
如图,圆B切y轴于原点O,过定点A(-
,0)作圆B的切线交圆于点P，已知tan∠PAB=
,抛物线C经过A、P两点。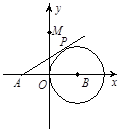
(1)求圆B的半径.
(2)若抛物线C经过点B,求其解析式.
(3)设抛物线C交y轴于点M,若三角形APM为直角三角形,求点M的坐标.
如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.
(1)当折痕的另一端F在AB边上时,如图(1).求△EFG的面积.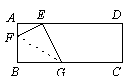
(2)当折痕的另一端F在AD边上时,如图(2).证明四边形BGEF为菱形,并求出折痕GF的长.
一家化工厂原来每月利润为120万元，从今年1月起安装使用回收净化设备（安装时间不计），一方面改善了环境，另一方面大大降低原料成本.据测算，使用回收净化设备后的1至x月（1≤x≤12）的利润的月平均值w（万元）满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平。
（1）设使用回收净化设备后的1至x月（1≤x≤12）的利润和为y,写出y关于x的函数关系式，并求前几个月的利润和等于700万元？
（2）当x为何值时，使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等？
（3）求使用回收净化设备后两年的利润总和。