某发电厂共有6台发电机发电，每台的发电量为300万千瓦/月．该厂计划从今年7月开始到年底，对6台发电机各进行一次改造升级．每月改造升级1台，这台发电机当月停机，并于次月再投入发电，每台发电机改造升级后，每月的发电量将比原来提高20%．已知每台发电机改造升级的费用为20万元．将今年7月份作为第1个月开始往后算，该厂第x（x是正整数）个月的发电量设为y（万千瓦）．
（1）求该厂第2个月的发电量及今年下半年的总发电量；
（2）求y关于x的函数关系式；
（3）如果每发1千瓦电可以盈利0.04元，那么从第1个月开始，至少要到第几个月，这期间该厂的发电盈利扣除发电机改造升级费用后的盈利总额ω1（万元），将超过同样时间内发电机不作改造升级时的发电盈利总额ω2（万元）？
（本题共10分）如图，点P、Q在数轴上表示的数分别是－8、4，点P以每秒2个单位的速度
运动，点Q以每秒1个单位的速度运动．设点P、Q同时出发，运动时间为t秒．
（1）若点P、Q同时向右运动2秒，则点P表示的数为_______，点P、Q之间的距离是______个单位；
（2）经过__________秒后，点P、Q重合；
（3）试探究：经过多少秒后，点P、Q两点间的距离为14个单位．
（本题共8分）某原料仓库一天的原料进出记录如下表（运进用正数表示，运出用负数表示）：
| 进出数量 （单位：吨） |
－3 |
4 |
－1 |
2 |
－5 |
| 进出次数 |
2 |
1 |
3 |
3 |
2 |
（1）这天仓库的原料比原来增加了还是减少了？请说明理由；
（2）根据实际情况，现有两种方案：
方案一：运进每吨原料费用5元，运出每吨原料费用8元；
方案二：不管运进还是运出费用都是每吨原料6元；
从节约运费的角度考虑，选用哪一种方案比较合适．
（3）在（2）的条件下，设运进原料共a吨，运出原料共b吨，a、b之间满足怎样的关系时，两种方案的
运费相同．
（本题共6分）已知当x＝－1时，代数式2mx3－3mx＋6的值为7．
（1）若关于
的方程2my＋n＝11－ny－m的解为y＝2，求n的值；
（2）若规定[a]表示不超过a的最大整数，例如[4.3]＝4，请在此规定下求[m－
n]的值．
（本题共6分）观察下列各式的计算结果：
1－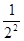
＝1－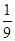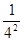
＝
＝
×
1－
＝1－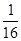
＝
＝
×
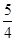1－
＝1－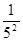
＝
＝×
1－
＝1－
＝
＝
×
……
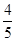（1）用你发现的规律填写下列式子的结果：
1－
＝ × ；1－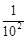
＝ × ；
（2）用你发现的规律计算：
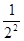（1－）×（1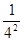－）×（1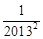－）×…×（1－
）×（1－
）．
（本题4分）把下列各数分别填入相应的集合内：
－2.5，0，8，－2，
，
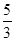，－0.5252252225…（每两个5之间依次增加1个2）．
（1）正数集合：｛…｝；
（2）负数集合：｛…｝；
（3）整数集合：｛…｝；
（4）无理数集合：{…}．