如图1,在平面直角坐标系xOy中,点M为抛物线 的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线 绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), .
.
①写出C点的坐标:C( , )(坐标用含有t的代数式表示);
②若点C在题(2)中旋转后的新抛物线上,求t的值.
(达州)(本题12分)如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数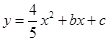 的图象经过A、C两点.
的图象经过A、C两点.
(1)求该二次函数的表达式;
(2)F、G分别为x轴、y轴上的动点,首尾顺次连结D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否存在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.
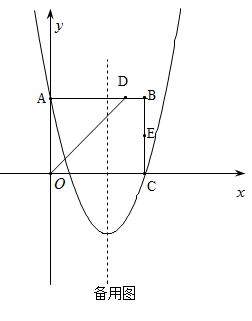
(南充)如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1, ,
,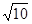 ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.
(南充)已知抛物线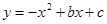 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线 (
(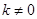 )与抛物线相交于两点M(
)与抛物线相交于两点M(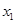 ,
, ),N(
),N( ,
,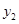 )(
)( ),当
),当 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.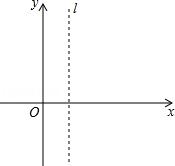
(成都)(本小题满分10分)如图,一次函数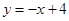 的图象与反比例函数
的图象与反比例函数 (
( 为常数,且
为常数,且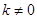 )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
(成都)(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HG•HB的值.