某公司要把240吨白砂糖运往某市的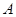 、
、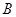 两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往
两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往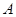 地的运费为:大车630元/辆,小车420元/辆;运往
地的运费为:大车630元/辆,小车420元/辆;运往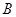 地的运费为:大车750元/辆,小车550元/辆.
地的运费为:大车750元/辆,小车550元/辆.
(1)求两种货车各用多少辆;
(2)如果安排10辆货车前往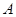 地,其中调往
地,其中调往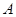 地的大车有
地的大车有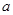 辆,其余货车前往
辆,其余货车前往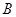 地,若设总运费为
地,若设总运费为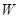 ,求W与
,求W与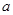 的关系式(用含有
的关系式(用含有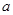 的代数式表示W).
的代数式表示W).
已知等腰三角形 中, 的平分线与 边交于点 , 为 的内切圆 与 边的切点,作 ,交 于点 .
证明: 是 的切线.
如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 是 的直径,连接 .
(1)求证: ;
(2)若 于点 ,求 的值.

如图所示, 是 的直径,点 是 上不同的两点,直线 交线段 于点 ,交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.

点 到图形 (可以是线段、三角形、圆或不规则图形等)的距离是指点 与图形 中所有点连接的线段中最短线段的长度.如图①中的两个虚线段 的长度都表示点 到图形 的距离.
如图②,在平面直角坐标系 中, 的三个顶点坐标分别为 ,点 从原点出发,以每秒 个单位长度的速度向 轴的正方向运动了 .
(1)当 时,求点 到 的距离;
(2)当点 到 的距离等于线段 的长度时,求 的取值范围;
(3)当点 到 的距离大于 时,求 的取值范围.

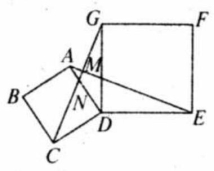
如图,四边形 都是正方形,连接 与 相交于点 与 相交于点 .求证:
(1)
(2) .