点P到图形Q（可以是线段、三角形、圆或不规则图形等）的距离是-优题课

题文

点 $P$ 到图形 $Q$ （可以是线段、三角形、圆或不规则图形等）的距离是指点 $P$ 与图形 $Q$ 中所有点连接的线段中最短线段的长度.如图①中的两个虚线段 $PQ$ 的长度都表示点 $P$ 到图形 $Q$ 的距离.

如图②，在平面直角坐标系 $xOy$ 中， $△ ABC$ 的三个顶点坐标分别为 $A (2, 1), B (0, 3), C (6, 3)$ ，点 $P$ 从原点出发，以每秒 $1$ 个单位长度的速度向 $x$ 轴的正方向运动了 $t s$ .

（1）当 $t = 0$ 时，求点 $P$ 到 $△ ABC$ 的距离；

（2）当点 $P$ 到 $△ ABC$ 的距离等于线段 $AP$ 的长度时，求 $t$ 的取值范围；

（3）当点 $P$ 到 $△ ABC$ 的距离大于 $\sqrt{5}$ 时，求 $t$ 的取值范围.

科目数学题型解答题难度较难

登录免费查看答案和解析

相关试题

解方程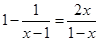

先化简，再求值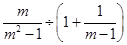：，其中．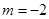

一包装礼盒是底面为正方形的无盖立体图形，其展开图如所示：是由一个正方形与四个正六边形组成，已知正六边形的边长为a，甲、乙两人分别用长方形和圆形硬板纸裁剪包装纸盒．
（1）问甲、乙两人谁的硬板纸利用率高，请通过计算长方形和圆的面积说明原因。
（2）你能设计出利用率更高的长方形硬板纸吗？请在展开图外围画出长方形硬板纸形状。

定义为函数的 “特征数”．如：函数y=x²－2x+3的“特征数”是{1，－2，3}，函数y=2x+3的“特征数”是{0，2，3}，函数y=－x的“特征数”是{0，－1，0}．
（1）将“特征数”是的函数图象向上平移2个单位，得到一个新函数，这个函数的解析式是；
（2）在（1）中，平移前后的两个函数分别与y轴交于O、A两点，与直线分别交于C、B两点，判断以A、B、C、O四点为顶点的四边形形状，并说明理由。
（3）若（2）中的四边形（不包括边界）始终覆盖着“特征数”是的函数图象的一部分，求满足条件的实数b的取值范围？

在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF．连接AF并延长交x轴的正半轴于点B，连接OF，设OD＝t．

（1）求tan∠FOB的值；
（2）用含t的代数式表示△OAB的面积S；

试卷网试题网古诗词网作文网范文网