定义 为函数
为函数 的 “特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}.
的 “特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}.
(1)将“特征数”是 的函数图象向上平移2个单位,得到一个新函数,这个函数的解析式是 ;
的函数图象向上平移2个单位,得到一个新函数,这个函数的解析式是 ;
(2)在(1)中,平移前后的两个函数分别与y轴交于O、A两点,与直线 分别交于C、B两点,判断以A、B、C、O四点为顶点的四边形形状,并说明理由。
分别交于C、B两点,判断以A、B、C、O四点为顶点的四边形形状,并说明理由。
(3)若(2)中的四边形(不包括边界)始终覆盖着“特征数”是 的函数图象的一部分,求满足条件的实数b的取值范围?
的函数图象的一部分,求满足条件的实数b的取值范围?
如图,已知直线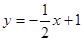 交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
请直接写出点C,D的坐标;
求抛物线的解析式
若正方形以每秒
 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围在(3)的条件下,抛物线与正方形一起平移,同时D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
如果两个正数 ,即
,即 ,有下面的不等式:
,有下面的不等式: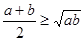 当且仅当
当且仅当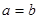 时取到等号
时取到等号
我们把 叫做正数
叫做正数 的算术平均数,把
的算术平均数,把 叫做正数
叫做正数 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知 ,求函数
,求函数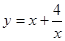 的最小值。
的最小值。
解:令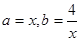 ,则有
,则有 ,得
,得 ,当且仅当
,当且仅当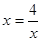 时,即
时,即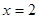 时,函数有最小值,最小值为
时,函数有最小值,最小值为 。
。
根据上面回答下列问题已知
 ,则当
,则当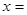 时,函数
时,函数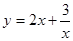 取到最小值,最小值
取到最小值,最小值
为用篱笆围一个面积为
 的矩形花园,问这个矩形的长、宽各为多少时,所
的矩形花园,问这个矩形的长、宽各为多少时,所
用的篱笆最短,最短的篱笆周长是多少已知
 ,则自变量
,则自变量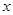 取何值时,函数
取何值时,函数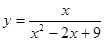 取到最大值,最大值为多少?
取到最大值,最大值为多少?
我们知道:直角三角形斜边上的中线等于斜边的一半,说明斜边上的中线可把直角三角形分成两个等腰三角形(图①)。又比如,顶角为36°的等腰三角形也能分成两个等腰三角形(图②)。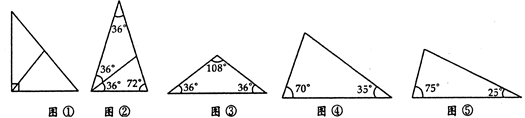
试试看,你能把图③、图④、图⑤中的三角形分成两个等腰三角形吗
△ABC中,有一内角为36°,过某一顶点的直线将△ABC分成两个等腰三角形,则满足上述条件的不同形状(相似的认为是同一形状)的△ABC最多有5种,除了图②、图③中的两种,还有三种,请你画出来
某花农培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元求甲、乙两种花木每株成本分别为多少元
根据市场调研,1株甲种花木的售价为760元,1株乙种花木的售价为540元,该花农决定在成本不超过30000元的前提下培育甲乙两种苗木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21600元,花农有哪几种具体的培育方案?
定义:如果一个数的平方等于-1,记为 =-1,这个数i叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
=-1,这个数i叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为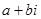 (a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: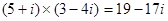
填空:
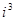 ="_________,"
="_________," 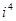 =____________
=____________计算:
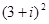
试一试:请利用以前学习的有关知识将
 化简成
化简成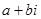 的形式.
的形式.
10年中考模拟卷改编