如果两个正数
，即
，有下面的不等式：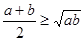
当且仅当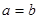
时取到等号
我们把
叫做正数的算术平均数，把
叫做正数的几何平均数，于是上述不等式可表述为：两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用，是解决最值问题的有力工具。下面举一例子：
例：已知
，求函数
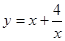的最小值。
解：令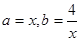
，则有
，得
，当且仅当
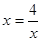时，即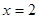
时，函数有最小值，最小值为
。
根据上面回答下列问题已知
，则当
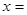时，函数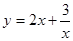
取到最小值，最小值
为 用篱笆围一个面积为
的矩形花园，问这个矩形的长、宽各为多少时，所
用的篱笆最短，最短的篱笆周长是多少已知
，则自变量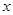
取何值时，函数
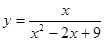取到最大值，最大值为多少？
观察下面的图形（每个正方形的边长均为1）和相应的等式，探究其中的规律：
（1）写出第五个等式，并在右边给出的五个正方形上画出与之对应的图示；
（2）猜想并写出与第n个图形相对应的等式．
出租车司机小李某天下午营运全是在东西走向的人民大道上进行的．如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：
+15，﹣2，+5，﹣1，+10，﹣3，﹣2，+12，+4，﹣5，+6
（1）将最后一名乘客送到目的地时，小李距下午出车时的出发点多远？
（2）若汽车耗油量为3升/千米，这天下午小李开车共耗油多少升？
如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数．请你画出它的主视图与左视图．
某班10名学生在一次数学测验中的成绩以90分为标准，超过的分数记为正数，不足的分数记为负数，记录如下：﹣7，﹣10，+9，+2，﹣1，+5，﹣8，+10，+4，+9．求他们的平均成绩．
某天，小明和小亮利用温差法测量紫金山一个山峰的高度，小明测得山顶温度为﹣1.1℃，同时，小亮测得山脚温度是1.6℃，已知该地区高度每增加100m，气温大约降低0.6℃．
（1）山脚比山顶高了多少度？
（2）这个山峰的高度大约是多少米？