已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,
求:(1)圆心O到AQ的距离;
(2)线段EF的长.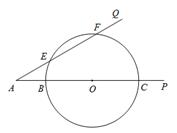
如图,已知A、B、C、D四点均在以BC为直径的⊙O上,AD∥BC,AC平分∠BCD,∠ADC=120°,BC=4.
(1)求扇形ODC的面积;
(2)求四边形ABCD的周长.
如图所示,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.
请你依据右面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘:

(1)用树状图表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率。
如图,抛物线 与直线
与直线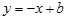 交于A,C两点,与x轴交于点A,B.点P为直线AC下方抛物线上的一个动点(不包括点A和点C),过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP.设点P的横坐标为m.
交于A,C两点,与x轴交于点A,B.点P为直线AC下方抛物线上的一个动点(不包括点A和点C),过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP.设点P的横坐标为m.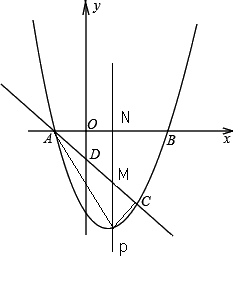
(1)求b的值;
(2)用含m的代数式表示线段PM的长并写出m的取值范围;
(3)求△PAC的面积S关于m的函数解析式,并求使得△APC面积最大时,点P的坐标;
(4)直接写出当△CMP为等腰三角形时点P的坐标.
如图,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.