甲、乙两车都从A地前往B地，如图分别表示甲、乙两车离A地的距离S（千米）与时间t（分钟）的函数关系.已知甲车出发10分钟后乙车才出发，甲车中途因故停止行驶一段时间后按原速继续驶向B地，最终甲、乙两车同时到达B地，根据图中提供的信息解答下列问题：
（1）甲、乙两车行驶时的速度分别为多少？
（2）乙车出发多少分钟后第一次与甲车相遇？
（3）甲车中途因故障停止行驶的时间为多少分钟？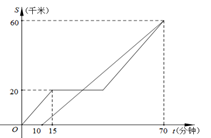
﹣（本题8分）“五一”期间，某超市贴出促销海报，内容如图1．在商场活动期间，王莉和同组同学随机调查了部分参与活动的顾客，统计了200人次的摸奖情况，绘制成如图2的频数分布直方图．
 |
|||
|
|||
﹣（本题8分）如图，在等腰梯形
中，
为底
的中点，连结
、
．
求证：
．
﹣（本题8分）化简：
如图，在平面直角坐标系
中，抛物线
向左平移1个单位，再向下平移4个单位，得到抛物线
.所得抛物线与
轴交于
两点（点
在点
的左边），与
轴交于点
，顶点为
.
（1）求
的值；
（2）求直线AC的函数解析式。
（3）在线段
上是否存在点
，使
与
相似.若存在，求出点的坐标；若不存在，说明理由.
(9分)如图，把△ABC置于平面直角坐标系中，请你按以下要求分别画图：
(1)画出△ABC向下平移5个单位长度得到的△A1B1C1；
(2)画出△ABC绕原点O逆时针旋转90º得到的△A2B2C2；
(3)画出△ABC关于原点O对称的△A3B3C3．