某校举行综合知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有6次答题的机会,选手累计答对4题或答错3题即终止其初赛的比赛,答对4题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响).
(Ⅰ)求选手甲回答一个问题的正确率;
(Ⅱ)求选手甲可以进入决赛的概率.
(本小题满分13分)已知等比数列 的公比为
的公比为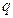 ,前
,前 项和为
项和为 ,且
,且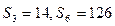 ,现若以
,现若以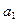 为首项
为首项 ,以公比
,以公比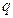 作为公差d构造新的等差数列
作为公差d构造新的等差数列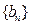
(1)求通项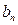 (2)记
(2)记 ,证明
,证明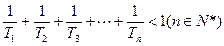
(本小题满分12分)已知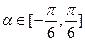 且
且 ,请求出
,请求出 与
与 的值
的值
(本小题满分12分)如图所示,△ABC中,∠A=60°、∠C=45°,BC=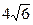 ,现点D在AC边上运动,点E在AB边上运动(不与端点重合)且AD=BE=
,现点D在AC边上运动,点E在AB边上运动(不与端点重合)且AD=BE= ,设△ADE面积为S
,设△ADE面积为S
(1)写出函数式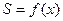 ,并标出定义域。
,并标出定义域。
(2)求出 取何值时,S有最大值,并求之。
取何值时,S有最大值,并求之。
(本小题满分12分)函数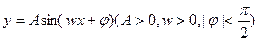 的图像上相邻的最高点与最低点的坐标分别为
的图像上相邻的最高点与最低点的坐标分别为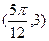 和
和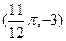 。 (1)求出
。 (1)求出 的解析式。(2)找出
的解析式。(2)找出 图像的对称中心和
图像的对称中心和 的递增区间。
的递增区间。
四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB= ,用
,用 表示∠ASD,求
表示∠ASD,求