如图,在平面直角坐标系中,己知点O(0,0),A(5,0),B(4,4).
(1)求过O、B、A三点的抛物线的解析式.
(2)在第一象限的抛物线上存在点M,使以O、A、B、M为顶点的四边形面积最大,求点M的坐标.
(3)作直线x=m交抛物线于点P,交线段OB于点Q,当△PQB为等腰三角形时,求m的值.
如图,∠ACB=∠CDE=90°,B是CE的中点,∠DCE=30°,AC=CD.求证:AB∥DE.
在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图28-1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.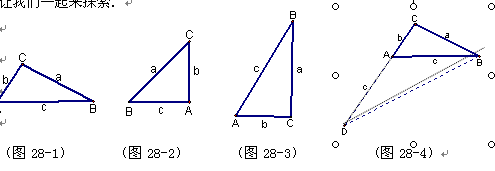
我们先从特殊的倍角三角形入手研究.请你结合图形填空:
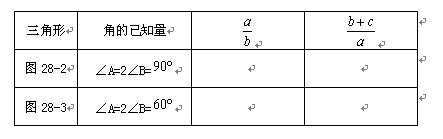
如图28-4,对于一般的倍角△ABC,若∠CAB=2∠CBA ,∠CAB、∠CBA、∠C的对边分别记为a、b、c,a、b、c三边有什么关系呢?请你作出猜测,并结合图28-4给出的辅助线提示加以证明.
如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为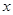 轴、
轴、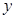 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在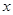 轴上),抛物线
轴上),抛物线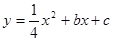 经过A、C两点,与
经过A、C两点,与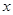 轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.求B点坐标;
求证:ME是⊙P的切线;
设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;②若FQ=
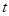 ,△ACQ的面积 S△ACQ=
,△ACQ的面积 S△ACQ=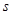 ,直接写出
,直接写出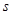 与
与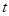 之间的函数关系式.
之间的函数关系式.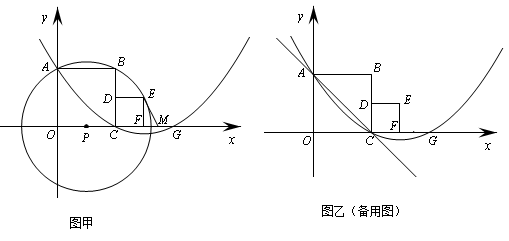
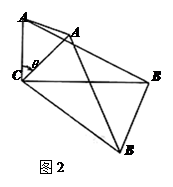
在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为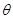 (0°<
(0°<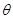 <180°),得到△A′B′C.
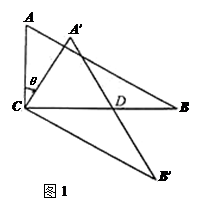
<180°),得到△A′B′C.如图(1),当AB∥CB′时,设A′B′与CB相交于点D.证明:△A′CD是等边三角形;
如图(2),连接A′A、B′B,设△ACA′ 和△BCB′ 的面积分别为S△ACA′ 和S△BCB′.求证:S△ACA′ :S△BCB′ =1:3;
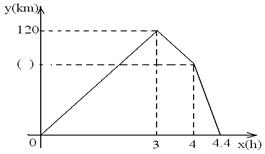
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.将图中()填上适当的值,并求甲车从A到B的速度.
求从甲车返回到与乙车相遇过程中y与x的函数关系式,并写出自变量取值范围.
求出甲车返回时行驶速度及AB两地的距离.